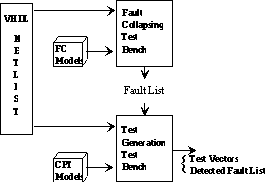
Figure 1. Test Environment

Figure 1. Test Environment
TYPE.GATE ID [ SINGLE STUCK FAULT LIST ] ... AND2( 108 ) [ I1:none ;I2:sa_1 ;O1:sa_1 ] OR2 ( 109 ) [ I1:none ;I2:none ;O1:sa_0 ] NOR2( 111 ) [ I1:none ;I2:sa_0 ;O1:sa_1 ] NOT ( 112 ) [ O:sa_1, sa_0 ] ... |
Tests Applied: 011111000101011 011100100100010 111100010001000 100010101000000 . . . Resulting fault coverage: 88% Faults that remain undetected are: AND2( 76 ) [ I2:sa_1 ] OR2 ( 23 ) [ O1:sa_0 ] NOR2( 45 ) [ I1:sa_1 ] NAND2( 48 ) [ I2:sa_0 ; O1:sa_1 ] . . . |
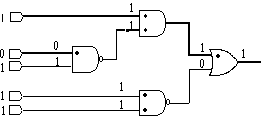
Figure 4. Example of CPT in a fanout-free circuit
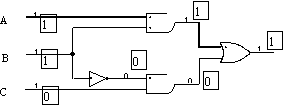
Figure 5. CPT with re-convergent fanout
In the original critical path tracing method [1], primary input values are propagated to all circuit lines. The circuit is traced from output to input for identifying critical lines in a manner similar to what was described in the previous section. In the process of this tracing, when a fanout is encountered, a simulation phase will determine if the effect of changing the value of a fanout stem will be marked as critical. In order to reduce the size of the part of the circuit that is simulated, a partitioning of the circuit is done to simulate only up to the point whose effect on the output is known. From the above discussion it is clear that critical path tracing by this method requires much forward simulation and backward propagation in an iterative fashion. In addition, partitioning of the circuit into isolated parts with inputs influenced by fanout stem and outputs influencing the primary output is a time consuming process. Above all, the case mentioned before, in which a fanout stem can be critical even if none of its branches are critical, cannot be handled by the standard CPT method. This is because, the method requires a critical path through branches to reach to a fanout.
Considering the problems associated with the original critical path tracing algorithm, we have developed a new method that eliminates the need for any partitioning or partial simulation of the circuit. In one pass CPT, simulation is only necessary at the beginning when a test vector is applied. Decision to mark a stem as critical will be based on the information that is passed from gates that are driven by the fanout branches back to the fanout node. In general one pass CPT is centered around the facts that 1) A gate with critical output locally decides on its input lines being critical, and 2) Fanout stems require information from all their branches before they can declare a stem as being critical. Therefore gates, interconnecting lines and fanout nodes must cooperate in providing necessary information to gates and fanout nodes.
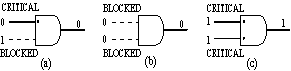
 Figure 7. Gate notations
Figure 7. Gate notations
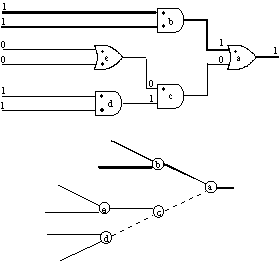 Figure 8. Critical path graph
Figure 8. Critical path graph
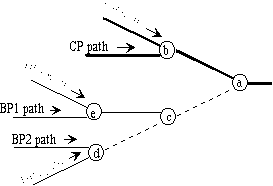 Figure 9. Path kinds
Figure 9. Path kinds
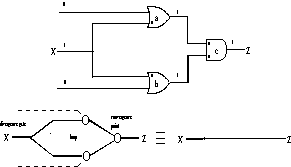 Figure 10. Rule a replaces two converging critical paths
Figure 10. Rule a replaces two converging critical paths
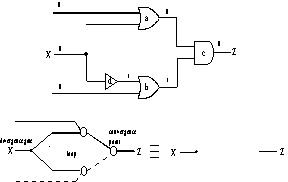
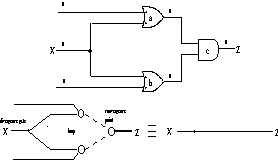 Figure 12. Rule c replaces two converging Bps with a CP
Figure 12. Rule c replaces two converging Bps with a CP
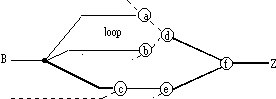
 (a)
(a)
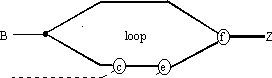 (a)
(a)

TYPE fsim IS RECORD logic : imp; path_info : bkt; END RECORD; |
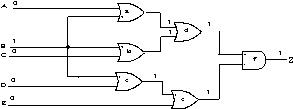
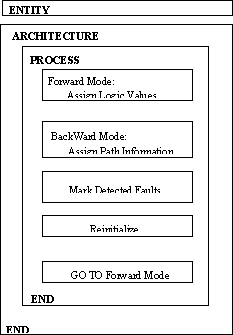 Figure 16. General CPT model structure
Figure 16. General CPT model structure
............ WAIT UNTIL i1.logic /= 'U' AND i2.logic /= 'U'; in1 := i1.logic; in2 := i2.logic; out1 := in1 NAND in2; o.logic <= out1; .............. |
............ --- initialization i1 <= none_U; i2 <= none_U; o <= none_U; --- wait until all lines in circuit initialized. WAIT FOR 10 PS; tn := tn + 1; ........ |
......... ELSIF temp_o(1,1) > -1 THEN IF in1 = '0' AND in2 = '1' THEN temp_i1 := added_node(temp_o,id); temp_i2 := increment_depth(temp_o,id); ELSIF in1 = '1' AND in2 = '0' THEN temp_i1 := increment_depth(temp_o,id); temp_i2 := added_node(temp_o,id); ELSIF in1 = '0' AND in2 = '0' THEN temp_i1 := increment_depth(temp_o,id); temp_i2 := temp_i1; ELSE .......... |
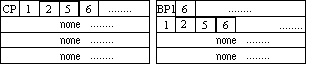
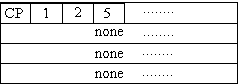 Figure 20. A path information example
Figure 20. A path information example
IF temp_o(1,1) = -1 THEN IF in1 = '1' AND in2 = '0' THEN temp_i1 := uncp; temp_i2 := temp_o; ELSIF in1 = '0' AND in2 = '1' THEN temp_i1 := temp_o; temp_i2 := uncp; ELSIF in1 = '0' AND in2 = '0' THEN temp_i1 := uncp; temp_i2 := uncp; ELSE temp_i1 := temp_o; temp_i2 := temp_o; END IF; |
FUNCTION backtracing (paths : int_4by20_vector) RETURN int_4by20 IS VARIABLE temp1, temp2 : int_4by20_vector(paths'RANGE); VARIABLE depth, util1 : INTEGER := 0; . . . BEGIN . . . FOR i IN paths'RANGE LOOP --Finding deepest path IF depth < temp1(i)(1,1) THEN depth := temp1(i)(1,1); END IF; END LOOP; |
......................
IF depth > 0 THEN ------------- construct and reject
FOR i IN depth DOWNTO 1 LOOP
-- path with i depth will be constructed.
FOR j IN paths'RANGE LOOP
IF temp1(j)(1,1) = i THEN
FOR l IN j + 1 TO (paths'LENGTH - 1) LOOP
IF temp1(l)(1,1) = i THEN
replace_check (
temp1(j), temp1(l), constructed, connection);
IF connection THEN
temp1(j) := constructed;
temp1(l) := none;
END IF;
END IF;
END LOOP;
END IF;
END LOOP;
FOR j IN paths'RANGE LOOP
---- path with i-1 depth is rejected
IF temp1(j)(1,1) = i THEN -- by path with i depth.
FOR l IN paths'RANGE LOOP
IF temp1(l)(1,1) = (i - 1) THEN
remove_check (
temp1(j), temp1(l), constructed, connection);
IF connection THEN
temp1(l) := constructed;
END IF;
END IF;
END LOOP;
END IF;
END LOOP;
END LOOP;
END IF;
........
|
CKT
PO
TYPE g_faults; TYPE g_faults_ptr IS ACCESS g_faults; TYPE g_faults IS RECORD g_type : STRING (1 TO 6); id : POSITIVE; in_1 : faults; -- inverters use in1 in_2 : faults; out_1 : faults; link : g_faults_ptr; --for linked list; END RECORD; . . . SHARED VARIABLE fault_table : g_faults_ptr := NULL; |
Before repeating the process of initializing the CPT models and applying a new test vector, the test controller checks for a target fault coverage. If this is satisfied, the test process terminates. At this time the list of undetected faults is extracted from the fault linked list and reported to an output file. An example of this file is shown in Figure 2. Other information such as the number of accomplished fault coverage are also reported to this output file. If the test process is not to terminate, the PRPG clock is activated for it to generate another random test data. Reaching a given fault coverage or exhausting all random test data are two reasons for the test process to terminate. 5. Conclusion We have shown vhdl models for fault collapsing and the use of such models for psuedo random test generation. The emphasis here was on the CPT method and its implemntation. More work is being done on the psudo random test generation and will be reported in a later paper. This work is part of an on-going research on VHDL modeling strategies for test related applications and environments utilizing such models. In this work gate models for tasks such as test generation, fault collapsing, and fault simulation are being developed. REFERENCES: